En física, un vector (también llamado vector euclidiano o vector geométrico) es una herramienta geométrica utilizada para representar una magnitud física definida por su módulo (olongitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo). En matemáticas se define un vector como un elemento de un espacio vectorial, esta noción es más abstracta y para mucho espacios vectoriales no es posible representar a sus vectores mediante un módulo o longitud y una orientación (ver Espacio vectorial).
Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta dirigidos («flechas») en el plano 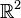 o en el espacio
o en el espacio  .
.
Son ejemplos de magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección hacia la que se dirige. La fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que opera. El desplazamiento de un objeto.
 puede también tener infinitas soluciones (si la recta está en el plano) o no tener solución (si no hay intersección).
puede también tener infinitas soluciones (si la recta está en el plano) o no tener solución (si no hay intersección). 





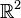 o en el espacio
o en el espacio  .
.